Uncategorized

Continuing their summer of “Everything Old is New Again”, ABC rolled out a new version of Card Sharks, the Goodson-Todman show that ran from 1976-1981, with a popular revival from 1986-1989.  (We are all in agreement that the 2001 version was a collective hallucination, right?)  While the show is slightly uneven, it captures enough to the charm of the original show to still be a good watch.

One of the major changes that they’ve made to the format is to the front game.  Instead of playing a best-of-three game of Acey Deucy, where the contestants must successfully call Higher or Lower on a row of 5 cards, it’s now a single round with a row of 10 cards.  I’ve previously discussed strategies about how to approach the Money Cards, but I think now’s a good time to take a closer look at the front game and see if we can figure out some strategies.

Before getting started, I had to make two assumptions about the front game in order to massively simplify things:

• Both players have a 50% chance of correctly answering a survey question correctly.  I have a hunch that the player going second on a question (the one saying higher or lower) wins more than their fair share, but that’s not something that I looked at in too much detail.
• Previously revealed cards cannot be considered when making your higher/lower decisions.  In the real game, you should keep count of how many high or low cards you’ve revealed, so that when you face an 8 (or in extreme cases, a 7 or 9), you know whether to go higher or lower based on what cards remain unseen.  However, trying to keep track of that would create too many game state possibilities, so we have to assume that the only card you’ve seen is the card you’re currently facing, and the next card could be any one of the other 51 in the deck.

With those limitations in mind, there are eight factors that determine the current state of a game:

• Your value of your current face-up card
• The number of cards that remain face down on your row
• The value of your base card
• The position of your base card
• Your opponent’s base card, if it’s been revealed
• The position of your opponent’s base card
• Whether or not you won the survey question
• The number of survey questions remaining in the round

Taking every possible combination of these eight variables that could happen in an actual game, I wound up with over 1.5 million different game states.  I (and by “I”, I mean a computer) then assembled them together into a Markov chain, which means that at any point in the game, if you have these eight pieces of data, you can determine the chances of victory regardless of how the game had proceeded in the past.

I’ve taken this giant Markov chain, and built a calculator out of it.  If you feed it the current game state, it will tell you not only your chances of victory, but also the best move to take at that time, whether it’s to play on, freeze, change your base card (if allowed), or pass during sudden death.

Let’s go step by step through an actual game, see whether the contestants chose the correct strategy, and if we can draw some broader strategic thoughts from the results. We’re going to look at the first game of the June 19^th episode, with players Kiko Gonzalez and Ann Hirsch.  Kiko played the red cards, while Ann played the blue.

Ann wins the first question, and reveals a Jack as her base card. She keeps it, and right off the bat, the first strategic decision of the match is a questionable one.

The one strategy that I see people get wrong all the time and doesn’t require anything fancier that simple counting is what base cards should be changed.  When you win a question, you can change your base card.  It’s a completely free option – there’s no downside to doing this other than the chance that you could worsen your position.  So, let’s evaluate each base card, and count the number of possibilities in each case that your position improves or worsens.

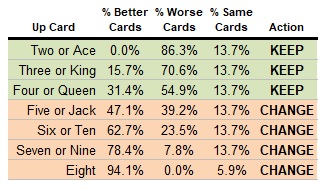
According to the raw numbers, the only cards you should keep as your base card are 2 through 4 and Queen through Ace.  Now, if you opt to keep a 5 or Jack, I’m not going to complain too much. You’re trading a couple of percentage points in improvement in your base card for a large amount of variance, so if you choose not to switch in this case, I can understand.  But the number of people I am seen who are willing to keep a 6 or 10 as their base card is staggering, and can’t be defended.

Anyway, Ann correctly calls her cards up to a 6 in slot #5 and freezes with 5 more places to go, all of which the calculator agrees with.  She’s got a 65.7% chance to win right now.

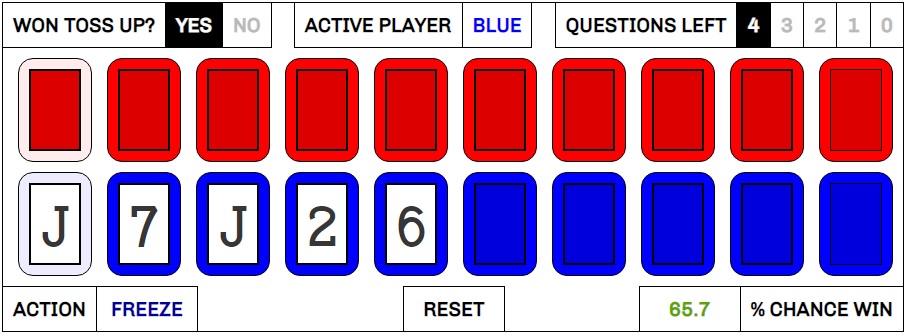
Kiko wins the second question, unveils a 10 as his base card, and doesn’t change (sigh). He calls lower on the next card, and is correct, revealing a 4. 

And here’s where the data completely shocks me.

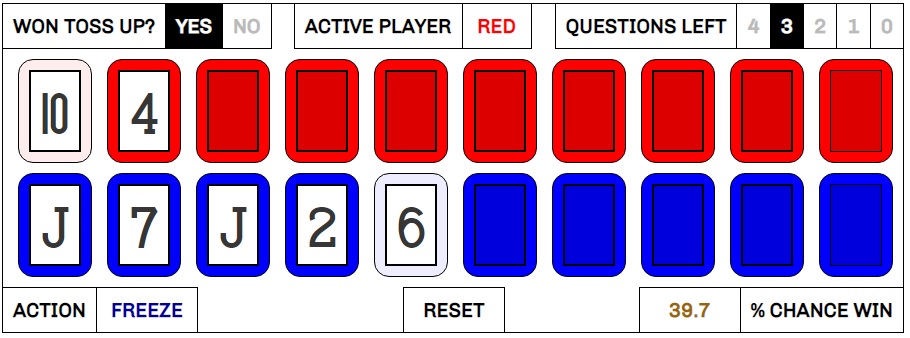
I literally had to double check this result, but, by a very slim margin of a couple tenths of a percent, freezing is the right play.  And it leads me into one of the bigger general strategic takeaways: play conservatively when you win the survey question, and play aggressively when you lose.

If you win a survey question, but proceed to miscall a card, you’re hurt in two different ways. Firstly, obviously, you’ve failed to make any progress on your board. But secondly, and even worse, you’ve given your opponent a free chance to play their cards. As a result, you need to play much more conservatively than in the case where you are the one receiving the free shot after your opponent messes up.

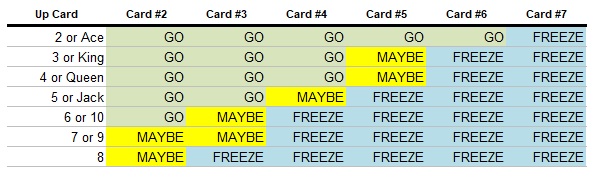
To illustrate this better, let’s assume that you win the first question of the match.  Based on the cards you get as you progress, when should you freeze?

For comparison’s sake, let’s say you lose the first question instead, but your opponent miscalls a card on their turn.  What should your strategy be now?

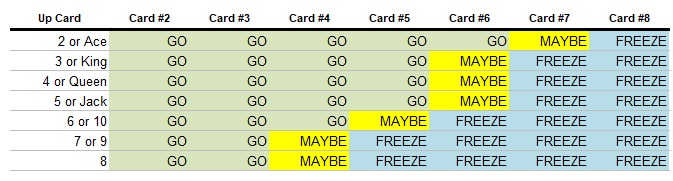
Not being at risk of giving your opponent a free crack at the cards allows you to play more aggressively.

Anyway, Kiko continues, and correctly calls the 9 as the third card.  He and the system agree that he should freeze here.  Things have improved for him, but he’s still a 40.7% underdog.

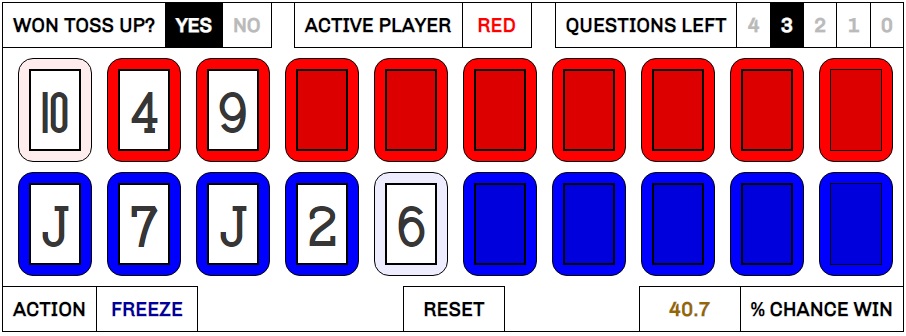
Ann wins control of the third question, changes the 6 (yay!) to a King, and goes on a tear, eventually ending up facing a 5 in the ninth card. 

One more correct call and she’s home free. The odds say to freeze at this point, giving her an 87.8% chance of winning the game in the next two questions. 

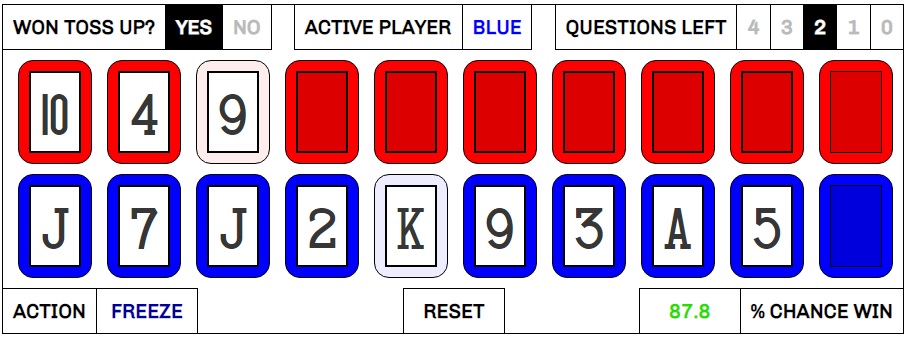
She opts to play on, hoping to convert on the 70.9% chance of calling a five correctly.  Unfortunately, she is punished for it, revealing a four as the next card and sending her back to her King.  Kiko doubles up with another 9 on the first call of his free shot, so nothing has changed except that we have one fewer question left in the game.  Ann is still a favorite, at a 61.3% to win.

Ann also wins the fourth question but doesn’t get too far into her row before missing.  Kiko gets another free run, and takes advantage, getting four calls right before facing a Jack as the seventh card in the row.

He opts to freeze, even though….

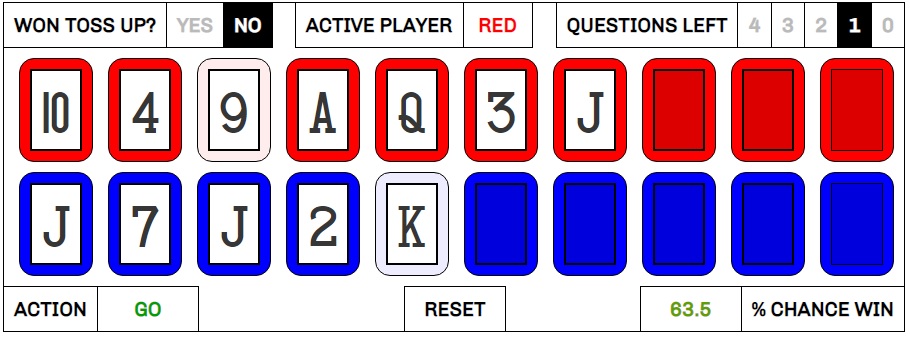
This may have been a better move earlier in the round, but we are going into sudden death on the next question.  If we freeze now and win the final question, we’re going to want to pass control of the cards to our opponent, who will only complete her row 23.7% of the time.  Yes, freezing here improves matters if we lose the next question.  We’re still a 37% underdog to win from this position, compared to a 7.9% chance if we were to fall back to the nine on our third card.  However, it’s better to combine that 37% chance now to try and finish the game, and fall back on getting the last question right if we can’t finish.

The game ends with Ann winning the last question and passing control of the cards back to Kiko, who can’t complete the row, giving Ann the victory.

As you can see just from this game, finding the right strategy can be difficult and non-intuitive. Both players made strategic missteps that seemed far from obvious to me before beginning this evaluation.

To get a better feel for it, I invite you to play around with the calculator.  Click on each card to choose their values and click the outer border to change each player’s base card.  You can also choose the active player, whether the active player won the question, and how many questions are left in the round.  With every legal game state, you’ll see what the system thinks is the best move, as well as what the active player’s chances are of getting to the Money Cards.