Probability Archives - Game Show Theory

Swimming with Card Sharks

June 26, 2019 by Dave 1 Comment

Continuing their summer of “Everything Old is New Again”, ABC rolled out a new version of Card Sharks, the Goodson-Todman show that ran from 1976-1981, with a popular revival from 1986-1989. (We are all in agreement that the 2001 version was a collective hallucination, right?) While the show is slightly uneven, it captures enough to the charm of the original show to still be a good watch.

One of the major changes that they’ve made to the format is to the front game. Instead of playing a best-of-three game of Acey Deucy, where the contestants must successfully call Higher or Lower on a row of 5 cards, it’s now a single round with a row of 10 cards. I’ve previously discussed strategies about how to approach the Money Cards, but I think now’s a good time to take a closer look at the front game and see if we can figure out some strategies.

Before getting started, I had to make two assumptions about the front game in order to massively simplify things:

Both players have a 50% chance of correctly answering a survey question correctly. I have a hunch that the player going second on a question (the one saying higher or lower) wins more than their fair share, but that’s not something that I looked at in too much detail.
Previously revealed cards cannot be considered when making your higher/lower decisions. In the real game, you should keep count of how many high or low cards you’ve revealed, so that when you face an 8 (or in extreme cases, a 7 or 9), you know whether to go higher or lower based on what cards remain unseen. However, trying to keep track of that would create too many game state possibilities, so we have to assume that the only card you’ve seen is the card you’re currently facing, and the next card could be any one of the other 51 in the deck.

With those limitations in mind, there are eight factors that determine the current state of a game:

Your value of your current face-up card
The number of cards that remain face down on your row
The value of your base card
The position of your base card
Your opponent’s base card, if it’s been revealed
The position of your opponent’s base card
Whether or not you won the survey question
The number of survey questions remaining in the round

Taking every possible combination of these eight variables that could happen in an actual game, I wound up with over 1.5 million different game states. I (and by “I”, I mean a computer) then assembled them together into a Markov chain, which means that at any point in the game, if you have these eight pieces of data, you can determine the chances of victory regardless of how the game had proceeded in the past.

I’ve taken this giant Markov chain, and built a calculator out of it. If you feed it the current game state, it will tell you not only your chances of victory, but also the best move to take at that time, whether it’s to play on, freeze, change your base card (if allowed), or pass during sudden death.

Let’s go step by step through an actual game, see whether the contestants chose the correct strategy, and if we can draw some broader strategic thoughts from the results. We’re going to look at the first game of the June 19^th episode, with players Kiko Gonzalez and Ann Hirsch. Kiko played the red cards, while Ann played the blue.

Ann wins the first question, and reveals a Jack as her base card. She keeps it, and right off the bat, the first strategic decision of the match is a questionable one.

The one strategy that I see people get wrong all the time and doesn’t require anything fancier that simple counting is what base cards should be changed. When you win a question, you can change your base card. It’s a completely free option – there’s no downside to doing this other than the chance that you could worsen your position. So, let’s evaluate each base card, and count the number of possibilities in each case that your position improves or worsens.

According to the raw numbers, the only cards you should keep as your base card are 2 through 4 and Queen through Ace. Now, if you opt to keep a 5 or Jack, I’m not going to complain too much. You’re trading a couple of percentage points in improvement in your base card for a large amount of variance, so if you choose not to switch in this case, I can understand. But the number of people I am seen who are willing to keep a 6 or 10 as their base card is staggering, and can’t be defended.

Anyway, Ann correctly calls her cards up to a 6 in slot #5 and freezes with 5 more places to go, all of which the calculator agrees with. She’s got a 65.7% chance to win right now.

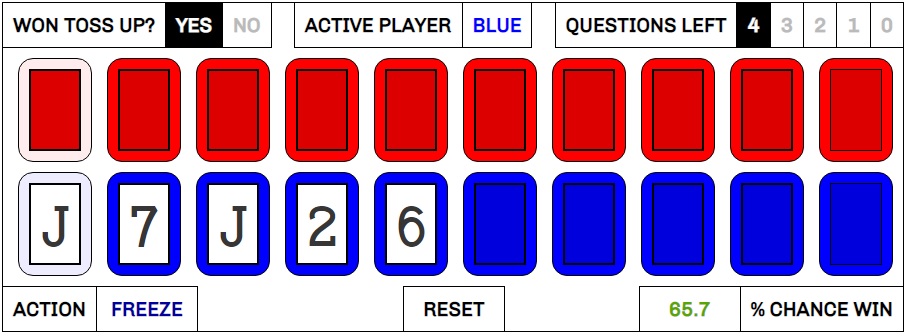
Kiko wins the second question, unveils a 10 as his base card, and doesn’t change (sigh). He calls lower on the next card, and is correct, revealing a 4.

And here’s where the data completely shocks me.

I literally had to double check this result, but, by a very slim margin of a couple tenths of a percent, freezing is the right play. And it leads me into one of the bigger general strategic takeaways: play conservatively when you win the survey question, and play aggressively when you lose.

If you win a survey question, but proceed to miscall a card, you’re hurt in two different ways. Firstly, obviously, you’ve failed to make any progress on your board. But secondly, and even worse, you’ve given your opponent a free chance to play their cards. As a result, you need to play much more conservatively than in the case where you are the one receiving the free shot after your opponent messes up.

To illustrate this better, let’s assume that you win the first question of the match. Based on the cards you get as you progress, when should you freeze?

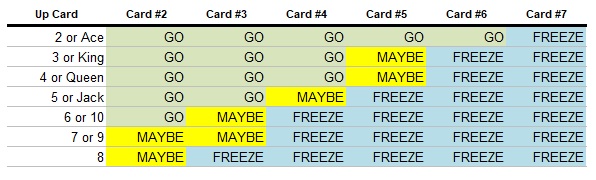
“MAYBE” is based upon your base card. The better your base card, the more willing you should be to play on.

For comparison’s sake, let’s say you lose the first question instead, but your opponent miscalls a card on their turn. What should your strategy be now?

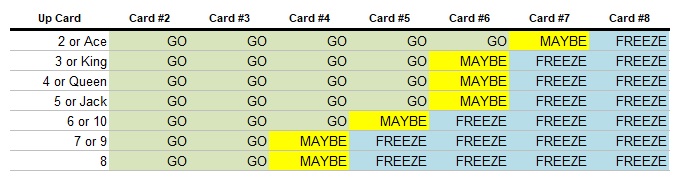
“MAYBE” in this situation is based on both your base card and your opponent’s base card.

Not being at risk of giving your opponent a free crack at the cards allows you to play more aggressively.

Anyway, Kiko continues, and correctly calls the 9 as the third card. He and the system agree that he should freeze here. Things have improved for him, but he’s still a 40.7% underdog.

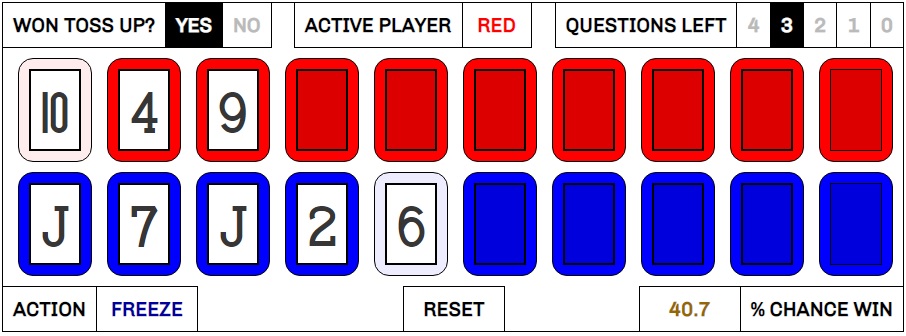
Ann wins control of the third question, changes the 6 (yay!) to a King, and goes on a tear, eventually ending up facing a 5 in the ninth card.

One more correct call and she’s home free. The odds say to freeze at this point, giving her an 87.8% chance of winning the game in the next two questions.

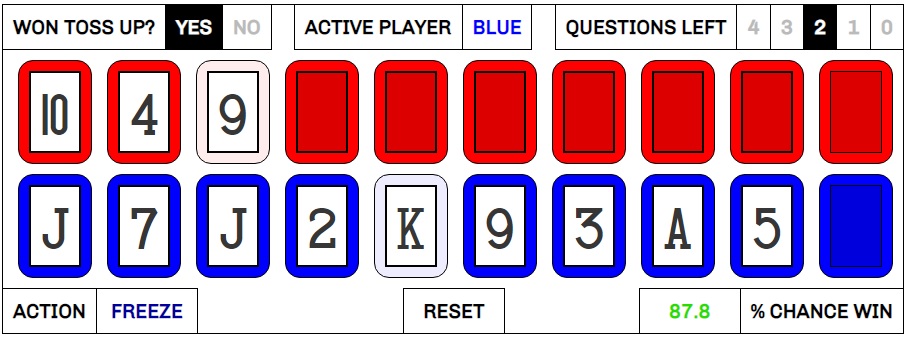
She opts to play on, hoping to convert on the 70.9% chance of calling a five correctly. Unfortunately, she is punished for it, revealing a four as the next card and sending her back to her King. Kiko doubles up with another 9 on the first call of his free shot, so nothing has changed except that we have one fewer question left in the game. Ann is still a favorite, at a 61.3% to win.

Ann also wins the fourth question but doesn’t get too far into her row before missing. Kiko gets another free run, and takes advantage, getting four calls right before facing a Jack as the seventh card in the row.

He opts to freeze, even though….

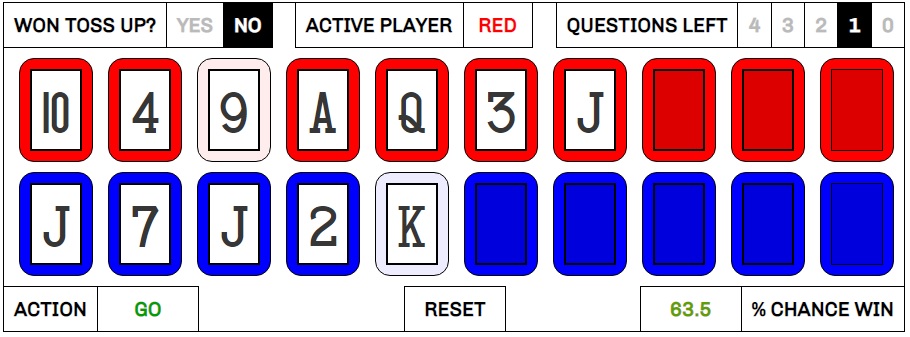
This may have been a better move earlier in the round, but we are going into sudden death on the next question. If we freeze now and win the final question, we’re going to want to pass control of the cards to our opponent, who will only complete her row 23.7% of the time. Yes, freezing here improves matters if we lose the next question. We’re still a 37% underdog to win from this position, compared to a 7.9% chance if we were to fall back to the nine on our third card. However, it’s better to combine that 37% chance now to try and finish the game, and fall back on getting the last question right if we can’t finish.

The game ends with Ann winning the last question and passing control of the cards back to Kiko, who can’t complete the row, giving Ann the victory.

As you can see just from this game, finding the right strategy can be difficult and non-intuitive. Both players made strategic missteps that seemed far from obvious to me before beginning this evaluation.

To get a better feel for it, I invite you to play around with the calculator. Click on each card to choose their values and click the outer border to change each player’s base card. You can also choose the active player, whether the active player won the question, and how many questions are left in the round. With every legal game state, you’ll see what the system thinks is the best move, as well as what the active player’s chances are of getting to the Money Cards.

Press Your Luck and Pot Roast: Exploiting the Big Board

June 12, 2019 by Dave 2 Comments

33 years on from its original cancellation, and 16 years after GSN revived it, Press Your Luck is back on our screens, introducing a new generation to the dreaded Whammy. Watching the premiere episode, I had two reactions. Firstly, of course, I was transported back to my childhood, watching the reruns of the original show during USA Network’s afternoon game show block. I certainly think PYL had a lot to do with fostering both my love for game shows and statistical analysis, so watching a very faithful rendition of it come to life in 2019 hit me with a great big wave of nostalgia, as I’m sure was the intention when they greenlit it.

The second reaction I had was the memory of an old story. I’ve heard this story told in a bunch of different ways, but Google tells me it’s usually called the Story about the Pot Roast:

One day after school a young girl noticed that her mom was cutting off the ends of a pot roast before putting it in the oven to cook for dinner. She had seen her mom do this many times before. When asked why her mom answered “I don’t know. it’s what my mom always did. Why don’t you ask your Grandma? ” Her grandmother, in turn, replied, I don’t know. That’s just the way my mom always cooked it. Why don’t you ask her?
So, undeterred, she called her great-grandmother, who was living in a nursing home and at last got an answer. Great Grandma explained. “When I was first married we had a very small oven, and the pot roast didn’t fit in the oven unless I cut the ends off!”

Why did this old saw come to mind as I watched? Because in their desire to keep the show as close to the original as possible, they managed to retain some of the flaws present in the gameplay of the original show. Flaws that were no doubt caused by the corners the producers had to cut to run the Big Board on the technology of the early 1980’s. Flaws that could have been easily be fixed with the technology of today.

Flaws that somebody could exploit.

Here’s a quick word about the rules of the game, if you need a refresher. The game is dominated by what’s known as the Big Board, a large display of 18 squares, arranged in a rectangular pattern. A flashing light randomly bounces from square to square, while the contents of each square also change in a regular pattern. The player who is in control of the Board may stop the Board’s movement at any time by hitting their button. The contents of the square that the flashing light stops on is what the player adds to their bank. It could be cash, it could be a prize, but it could also be a Whammy. Landing on a Whammy bankrupts the player, so it’s imperative to avoid the Whammy as often as possible.

The main game is played in two rounds, with two different board configurations. In the first round, there are 9 Whammies out of a possible 54 possible slides, which should lead you to a 1-out-of-6 chance of hitting a Whammy. However, two of the Whammies are located in one single space, which very slightly decreases the chances to 16.54%. The board configuration in round two adds a 10th Whammy, and the chances of hitting one of those suckers is 18.37%.

Can we come up with a viable strategy to hit a Whammy less often?

Fans of the game certainly know about the famous Michael Larson exploit, where a contestant on the original show memorized the finite number of paths that the bouncing light could take in order to always land on a space that never contained a Whammy. I have no doubt that the patterns of lights that flash on the Big Board today are as close to random as computationally possible, so trying to replicate Larson’s feat is a fool’s errand.

Instead, I noticed three flaws that they kept from the old show, no doubt to keep the show looking as close to the original as possible. These flaws taken together suggest a couple of strategies that one could use to land on the Whammy significantly less often than a player who is just randomly stopping the board.

Flaw 1: Every space on the board only contains three possible outcomes.

Back in the day, when they used slide projectors to create the Big Board, they had to limit the number of possible outcomes in each square. But nowadays, no such limit exists. They could have increased the potential number of outcomes to a huge number, or even have certain prizes move around the board, showing up in different squares. But, since they chose too keep the three-outcomes-per-square setup, we can quickly and easily enumerate all possible outcomes that a square can hold, and just as easily determine the chances of hitting a Whammy given any board configuration.

Flaw 2: All of the spaces change at the same time.

This was a flaw that was corrected by GSN in their revival, but has since returned. This means that, instead of the board being in a constant state of flux, there exists a small period of time where the board state freezes. If one is quick enough, one could theoretically count the number of Whammies currently present on the board, and in doing so not stop the board unless that number was in your advantage.

One thing we must keep in mind when creating a strategy is that we must stop the board within a reasonable amount of time. If we resolve not to stop the board unless there are zero Whammies showing, then we’re going to be waiting for quite a while, since that only happens on average once every 50 transitions. (For the purposes of this article, when I talk about a “transition”, I’m talking about the time when the spaces change their contents, not when the bouncing light changes squares.) Studio time is expensive, so even though they would edit the down time for broadcast, I’m sure the producers would have a word with if it took you two minutes to stop the board. Considering that, we want to have a strategy that will stop the board within a reasonable number of transitions most of the time. For the purposes of this article, I will define a “reasonable number of transitions” as stopping the board within 10 transitions or fewer 90% of the time.

Playing around with the percentages, I found that a strategy where you stop the board if there are 0 or 1 Whammies showing within the first seven transitions, and stopping after that when 2 or fewer Whammies are showing means that you’ll be hitting the buzzer within 10 transitions 90.7% of the time, and within 14 transitions over 99% of the time, which is good enough for me.

If we follow this strategy, there will be an average of 1.12 Whammies on the board when we hit the buzzer, which translates to a Whammy rate of 6.27%, which means instead of hitting a Whammy once out of about 6 spins, we are now hitting a Whammy once out of about 16 spins!

There is, however, one giant, glaring flaw in this strategy, and that’s those pesky limits of human ability. I took a stopwatch to last night’s episode, and calculated that the time between transitions of the board is about 4/5ths of a second. Thanks to the fact that the Whammies are always in bright yellow squares that stand out compared to all the other squares, it’s not too difficult to count their number within that time just using peripheral vision. However, determining if that number is lower than the threshold, and then send the signal from the brain to the hand to push the button to stop the board within that time is a very tough ask for everyone but the twitchiest of e-sports professionals.

So is there another strategy we can use? Yes, there is, taking advantage of a one more flaw that has been carried over from the old days.

Flaw 3: When a square transitions, it cannot display the same thing twice in a row.

In the past, in order to effect a transition, they had to change the slide that was projected onto a square. But nowadays, they are under no such limitation. If they wanted to, they could keep the displayed outcome of a square the same from transition to transition, but they chose not to.

What does this flaw mean for us? Well, we know that if a Whammy is currently displayed on a square, we know that when that square transitions, the Whammy will go away, leaving something else. Only one square in each of the first two rounds contains multiple Whammies. All of the other squares, if they currently contain a Whammy, are then guaranteed not to hold a Whammy once it transitions. So, if we can count the number of Whammies on currently the board, and that number is higher than average, then we should expect a lower than average number of Whammies to show up the next time the board transitions!

This strategy is much easier to execute. Thanks to the Whammy squares being visually different from the rest of the board, it is certainly possible to count the number of Whammies present within 0.8 seconds, which gives you another 0.8 second window to push the button once you see the board transition. Try this wit the GIFs on this page, or the next time you watch the show, and you’ll see that this seems very doable.

Let’s try to create a strategy using the same limitations as above. If in the first five transitions, you count five or more Whammies, you will want to hit the button after the next transition. Otherwise, hit it the transition after counting four or more Whammies. Following this strategy, you’ll still hit the button within 10 transitions 90% of the time. You’ll also decrease your Whammy rate from 16.54% to 11.46%, which is about 1 in 8.72 spins. The difference is smaller, but still pretty dramatic.

As I mentioned above, the board changes for round two, and adds another Whammy. With the increased odds, we need to create a new strategy following our usual restrictions. Thus, If you count 5 or more Whammies on the board in your first 8 transitions, stop the board on the following transition. After 8 transitions, drop that threshold to 4 Whammies. This strategy will still result in hitting the button within 10 transitions 90% of the time, and drops the Whammy rate from 18.37% to 13.17%, or about 7.6-to-1.

People expecting a Larsonesque strategy might be disappointed, but a person following this strategy will still hit 40% fewer Whammies compared to a person randomly stopping the board. If you’re hitting Whammies 40% less often than your opponents, I like your chances. As people like professional sports bettors or poker players would tell you, small advantages can add up to big wins.

Beating the Big Numbers on High Rollers

March 25, 2016 by Dave 7 Comments

Trebek and Lee. They’re cops!

When you think about dice and game shows, the show you probably think of first is the Heatter-Quigley show High Rollers, hosted by Alex Trebek and his awesome 70’s fro for two separate runs on NBC, and then again by Wink Martindale in 1987. Through every incarnation of the show, the bonus round remained the same: the Big Numbers. Based on the old gambling game Shut the Box, it heavily relied on luck, but also had some strategy in how you played it. It also seemed extremely difficult, as players rarely walked away winners. We wondered if the difficulty of the game was due to poor strategy, or if the game was simply stacked against the contestant. To answer that question, we first had to figure out just what the optimal strategy should be.

The rules are simple enough. The contestant is faced with the numbers 1 through 9. In order to win, they must eliminate each number, which they do by rolling two dice. After each die roll, the contestant chooses from the numbers they have remaining either a number or combination of numbers that equal to the number rolled, which are then eliminated from further consideration. If the contestant manages to eliminate all nine numbers before rolling a number that cannot be matched, they win the grand prize.

During the course of the game, the contestant can also earn “insurance markers”. Every time they roll doubles, they earn an insurance marker, which essentially give the contestant an extra life – if they roll a total which they cannot match, they may instead roll again. Contestants can use insurance immediately, even on the same roll that earned them the insurance.

The Big Numbers board in the 1987 revival, in all its glorious 80s-ness.

Sometimes you can only match a roll one way. But most of the time, especially in the first few rolls, you have several ways to match a total with the numbers remaining. For example, there are 12 possible ways of matching a roll of 12 on the first roll! Which of these 12 would give you the best chance of winning the game?

We decided to take a brute force approach to evaluating this game. Since there are nine different numbers, and each number has two states (either still on the board or removed), that means that there are 512 (2 to the 9th power) possible combinations of numbers that you could be left with at some point during the game. While that would be a large number to work out by hand, luckily we can make the computer do most of the heaving lifting for us.

First, we can trivially work out the probabilities of every situation where there are no choices to be made. For example, consider the situation where only the number 7 is lit up and we have no insurance markers. The only way to win in this case is to roll a 7. Seasoned gamblers would know that the chances of rolling 7 on a pair of dice is 16.66% chance, or ⅙. However we have to remember that not all non-seven rolls will lose the game – a roll of doubles grants an insurance marker that we could immediately cash in. That means that of the 36 possible rolls, 6 are winners, 6 let us roll again, and 24 are losers, which means the chances of winning are 6 / 30, or 20%.

Once we have these easy cases calculated, we can start working on the cases where we have a choice. We used an iterative process for this. We made up a list of all number combinations that we could not evaluate as above, and looked at each of them. If we came up with a case where every option’s chances of winning had not yet been determined, we skipped it for the moment. If we could figure out every choice’s chances of victory, we could then figure out which option would provide the greatest chance of victory, and then determine what the overall chances of winning were from that configuration of numbers.

For example, say we have the numbers 3, 4, and 7 left on the board. We could not have figured out the chances of victory from this position earlier, since if we roll a 7, we can do one of two things: take off the 3 and 4 leaving the 7, or remove the 7 and leave the 3 and 4. But now that we’ve determined the chances of winning from all of the simple cases, we can use those to figure out this case as well. We’ve already figured out that the chances of victory if we have a bare 7 left on the board is 20%. It turns out that the chances of victory with 3 and 4 on the board are slightly better: 20.83%. That means in this instance, we should eliminate the 7 if we roll a seven with the dice, since a board with a 3 and a 4 left on it would be easier to deal with than a board with only a 7 on it. Combine that with the chances of winning when we roll the other good numbers, none of which require making a choice (3, 4, 10, 11), we can determine that the overall chances of victory from this position are 7.64%.

After iterating through the list of unsolved configurations several times, we eventually discovered both the best strategy to use and the chances of winning from every possible combination of numbers. From the starting position, where all nine numbers are lit and you have no insurance markers, you have a 17.1% chance of knocking all the numbers off.

Gene has a 9.32% chance of winning right now. How’d he do?

Can we make any characterizations about the best strategy? In general, it seems that the best strategy is to remove the largest numbers from the board that you can from your roll. This means that on your first roll, if your roll is less than nine, you should remove just the number you rolled. If you roll 10 or more, you should remove the 9 and either the 1, 2, or 3, depending on if you rolled 10, 11, or 12.

I do say this is the best strategy in general, but there appear to be a large number of exceptions. Say you rolled a five to start with, and took off the 5. If on your second roll you rolled another five, you might be inclined, following the rule of thumb above, to knock off the 4 and the 1. Doing this leaves you with a 7.01% chance of winning. If instead you removed the 3 and 2, you’d have a 7.47% chance of winning. This is just one of many cases where following the general strategy is not optimal. We tried to figure out if there was a common thread to these exceptions, but nothing jumped out at us. Even so, We would expect that a person following the basic strategy and ignoring these exceptions would probably only cost themselves a few tenths of a percent on their overall winning percentage.

If you’d like to play around with these results, I’ve included a little widget at the end of this post for you to play with. Highlight the numbers remaining on the board and the number of insurance markers you have, and it’ll outline the best strategy to follow at that point, as well as your chances of victory. Have fun!

Chasing Down The Best Chaser

December 10, 2015 by Dave 7 Comments

Pictured Left to Right: Velma, Scooby, Daphne, Shaggy, Fred.

Earlier this year, Jenny Ryan joined the cast of the ITV hit show The Chase as the fifth resident chaser. The Vixen will take her place among trivia’s rogues gallery alongside Mark “The Beast” Labbett, Shaun “The Dark Destroyer” Wallace, Anne “The Governess” Hegerty, and Paul “The Sinnerman” Sinha. Given Jenny’s trivia bona fides (QI elf, Only Connect series champ, University Challenge, Mastermind, and Fifteen-to-One alumna), it’s no surprise that she fit right in alongside the others, who between them have over 700 episodes of experience with crushing the hopes and dreams of unlucky contestants. But, after all those episodes, who among them is the best at their job? Who’s the one you would least want to meet at night in a dark alley of trivia? (Note: Given that Ryan has not had much time to accumulate data, we will ignore her for the purposes of this question.)

The chasers have two chances to catch contestants and eliminate them during the show. First, they can eliminate contestants individually during each contestant’s head-to-head round. Finally, they can eliminate the team as a whole by catching them during the final chase. Let’s look at each round individually and see what data we can get.

Head-to-Head Round

During the head-to-head round, the contestant is tasked with getting multiple choice questions right, each correct answer allowing the contestant to take one step towards victory and earning money for the communal team bank. The chaser starts eight steps away from the finish. The contestant can choose to start either four, five, or six steps away from the finish (and thus starting with either a four, three, or two step head start on the Chaser), with the further starting locations worth more money. The Chaser and the contestant are asked the same questions, with each right answer bringing them closer to the finish line. If the contestant manages to stay ahead of the Chaser and reach the finish line, they put their earned cash into the communal bank, and earn a spot in the Final Chase at the end of the show. If the Chaser catches up to them before that happens, they don’t earn the money and are eliminated.

It is tough to get an accurate read on the Chaser’s abilities from the data that we have in this round. We are relying on the results provided by the Chase Wikia, which only gives a one-line summary of how each episode finished. It would be great if we could watch all 707 episodes from the first eight seasons of the show and keep detailed records of the Chaser’s correct answer rate, but that may be a project for when somebody finally invents the 28-hour day. Still, we do have a record of how often each Chaser catches a contestant in this round. Can we do anything with that?

Before we put too much stock in these numbers, I do want to share my reservations about it. First, we do not have the data of how many contestants opted to start with a two, three, or four step head start. We can assume that each chaser gets about the same amount of contestants to step closer or further away, but it introduces a small element of imprecision we can’t address.

Another issue that muddies the water is that some contestants are uncatchable. If a contestant answers every question correctly (or answers incorrectly a fewer amount of times than their head start), then the performance of the Chaser is moot. It will always be chalked up as a loss. It doesn’t seem right that there are times that a Chaser could answer every question correctly or every question incorrectly and have it look the same either way in the data.

Finally, the bigger issue is that these numbers are so close as not to be statistically significant. Even though each Chaser has faced down between 600 and 800 contestants each, that’s still too small of a sample size to say that these numbers are definitive. The margin of error of each of these numbers at a 95% confidence interval is around 3.5% percent, as illustrated in this chart.

In this graph, we’ve highlighted the margin of error in red, representing where we think each Chaser’s true value could fall within a 95% certainty. You can see that even Paul’s low mark could theoretically still be the highest among the four.

So it’s clear that this analysis isn’t the best determination of Chaser performance. Can we do better in the Final Chase?

Final Chase

Pictured Left to Right: Ginger, Baby, Scary, Sporty, Posh

After every contestant has had a chance to play head-to-head against the Chaser, those who survive are brought back to try and win the communal bank. The team is given 2 minutes to answer as many questions as they can. The Chaser then gets another two minutes to try to match the score set by the contestants. If they do that, then it’s game over for the team. If the Chaser falls short, then the surviving team members split the bank. To even the playing field, the contestants are given two major advantages. Firstly, they earn a head start equal to the number of surviving contestants. Secondly, anytime that the Chaser misses a question during their turn, the clock is stopped and the contestants get a chance to answer it themselves. If they get the question correct, they push the Chaser back one step.

The data we have for this round is of a much higher quality. We know how many contestants the team has left and how well they scored during their two minutes. We also have the Chaser’s final score, and how long the Chaser took to catch the team if the Chaser won. What we’d like to do is use the Chaser’s score as the performance metric in this round, but we’ll need to do a few things first to take care of the variable conditions of this round.

The most obvious place to start is by normalizing the amount of time each Chaser has to answer questions. Since the game is over as soon as the Chaser meets the score set by the contestants, we need to figure out what the Chaser would have scored had they had their full two minutes. That’s simple enough: We will give them credit for the missing time by assuming that they will continue to answer questions at the same rate. Thus, if a Chaser catches a team with a score of 15 with 30 seconds left, we will treat that as a score of 20. If the Chaser fails to catch the contestants, their score will not change, as they used the entire two minutes.

Now, there are a couple of issues with treating the scores this way. If a Chaser has to chase down a small score, it’s possible that they might take a couple of seconds extra to think about each question before answering. On the flip side, if they have to chase down a large score, they may rush and become prone to more mistakes. Also, (and I have no proof of this except my own anecdotal experience of watching the show) I feel that the host, Bradley Walsh, will speed up his reading of the questions if time is winding down and the Chaser is close to the target. While these are things we need to be aware of, I still feel comfortable about normalizing the scores in this way.

Pictured Left to Right: Niall, Liam, Harry, Louis, Zayn

The other thing we need to control for is the number of opponents that the Chaser is facing. Since the contestants get offered any questions that the Chaser misses, and their right answers are deducted from the Chaser’s score, the number of contestants left on the team has a direct impact on the Chaser’s final score. Analyzing the Chaser’s scores as a function of team size tells us that a two or three player team will earn around one more pushback than a one player team, while a full four player team earns around 1.5 pushbacks more than the single player. If the Chaser faces a multi-person team, we will give them credit for these extra pushbacks so the data is normalized to a Chaser facing a single player.

Now that we’ve eliminated all variables outside the control of the Chaser, here’s each Chaser’s average performance.

Mark, Anne, and Paul are all very close, but Shaun ends up averaging almost 2 questions less. This is borne out by using each chaser’s raw winning %: Mark, Anne, and Paul win about three-quarters of the time, while Shaun’s victory rate is only two-thirds.

This data does not suffer from the issues of the data from the head-to-head round. This data is a metric of raw performance on the part of the Chasers; we have eliminated any effects the contestants have on this score. It is also significant to a 95% confidence level. The margin of error on these numbers is between 0.6 and 0.7 of a question for each Chaser, which means that while we can’t say that Mark, Anne or Paul are better than one another, they all have performed better than Shaun.

Extrapolation

There’s something else that we can do with this data that’s pretty cool. To illustrate this, let’s take a look at a graph of the frequency of Mark’s normalized scores, rounded to the nearest whole number.

Say, that kinda looks like a bell curve, doesn’t it? Doing some normality testing on the data bears this hypothesis out; this data likely conforms to a normal distribution. The other Chasers’ data has the same feature. Therefore, since we know each Chasers’ average performance and standard deviation during the Final Chase, we can extrapolate upon this data and determine the odds of a Chaser beating any given score by fitting a normal distribution to each Chaser’s average score and standard deviation.

For example, let’s assume that a full team of 4 sets a score of 17 during their final chase. Not too shabby, right? What’s the likelihood that each Chaser will chase down that score?

Since our averages are normalized for a 1 person team, and this example uses a 4 person team, we will add 1.5 to their final score to represent the greater number of pushbacks that the team will score. So, the Chaser will have to score at least 18.5 points in order to catch the team. What is the team’s chance of victory against each Chaser?

Here you can see just how much an effect that two question difference between Shaun and the other three has. Facing Paul, Anne, or Mark, the team has less than a 1 in 4 chance of victory. Up against Shaun, the team will run out winners 42% of the time.

Here’s the full graph that shows the chance that a team will beat each Chaser based on their final score (before pushbacks).

Pictured Left to Right: Wasp, Hulk, Iron Man, Thor, Ant-Man

So who is the best Chaser? With the data we have right now, it’s hard to tell. I’d be inclined to call it a dead heat between Mark and Anne, with Paul just a nose behind them, and Shaun a bit further back. Despite this gap, I want to stress that Shaun is still an formidable opponent, and if the contestants facing him are expecting an easy game, they’re going to be disappointed. Time will tell how Jenny will fit into this group, but given her quizzing pedigree I expect her to do just as well as the other four regulars.

2015 Jeopardy Tournament of Champions: Semifinal Update

November 16, 2015 by Dave 23 Comments

Couple of random thoughts before revealing my predictions for the ToC Semifinals:

– My system did pretty darn well this year, getting 4 of the 5 winners of the semifinals correct. Granted, it wasn’t much of a radical prediction to say that Matt Jackson and Alex Jacob would win their games. However, I’d argue that Kerry Greene, despite nominally being the top seed in her game, was not an obvious favorite, nor would Catherine Hardee be easy to pick out as a favorite to win from the third lectern. The system’s one miss was favoring Greg Seroka and Kristin Sausville over the eventual winner from Tuesday’s game, Brennan Bushee, though to be fair Bushee won the game from last place by being the only player to get Final Jeopardy correct.
– The Wild Card cutoff point was higher than average this year at $14,000. The average over the history of the tournament (after doubling the scores of the pre-double dollars era) stood at $10,464. Anecdotally, I’d think that may be the effect of almost all players going into their games with the goal of not necessarily winning, but playing to hit a self-determined goal score that would earn them a wild card. With much more data out there about things like historical wild card totals, I wonder if this is going to lead to a situation where the wild card cutoff will always be higher than historically expected. Then again, last year’s cutoff was $9,100, and most of the data was available then too, so it’s just as likely there’s no great reason for this year’s cutoff being so much higher.
– I would love to know how the Jeopardy team selects the semifinal matchups. I’ve tried to come up with some set of seeding rules, but nothing I can find explains the matchups perfectly. The only rules that I know for sure are that players will not face their opponents from their quarterfinal match, and two people with the same first name will not play each other. This is different from the quarterfinals, where the games are fairly obviously seeded so that in each match one of the top 5 players (ranked by games and money won) plays one of the second five and one of the bottom five.
– I need to thank Andy Saunders of The Jeopardy Fan for his guesses as to what the semifinal matchups would be, which turned out to be correct and give me a little more time to run the numbers. Jeopardy didn’t officially release the matchups until Monday morning (as far as I saw through the official channels), which is slightly annoying for those of us in the game-show-data-analysis business.

Our prediction of Jackson vs. Jacob vs. [Seroka/Sausville/Hardee] isn’t going to be happening, since neither Greg Seroka nor Kristin Sausville made the second week, and Catherine Hardee is playing Matt Jackson in Wednesday’s game. Instead, the favorite for that third slot becomes Dan Feitel, winner of the Semifinal Matchup sweepstakes. He had the biggest movement in our prediction engine thanks to staying out of the path of the two juggernauts, increasing his chances of winning the tournament from 4% to 14%.

Alex dominated his quarterfinal game, becoming the only player to have a lock game last week. We see no reason to expect a different result from his semifinal matchup against Brennan Bushee and Vaughn Winchell.

If anybody is going to keep us from a final of M Jackson v. A Jacob v. AN Other, Catherine Hardee has the best chance of doing it. She could actually outbuzz Jackson, possibly the first time he’s ever had to face somebody who could do that. If she can keep her number of wrong answers down and take a few Daily Doubles, she could still certainly crash the finals. However, the smart money still has to be on Jackson winning this matchup.

Thanks to a slightly easier Semifinal matchup, Alex Jacob takes the tag of favorite by a clear margin over Jackson. Both men are close to 1-in-4 odds of taking the title. As prevously stated, Dan Feitel moves from his quarterfinal position of “best of the rest” into a solid third place thanks to avoiding the two favorites. Good luck to all participants, and here’s hoping that the games to come are just as fun, interesting, and exciting as last week’s games.

Lightning Round: Matt Jackson, New Jeopardy Record Holder?

October 9, 2015 by Dave Leave a Comment

So things have been quiet here for a few months. I’ve been very busy at work lately, but I do have a couple of articles that are very close to being finished that will be up in the next few weeks. One is a treatise on Daily Double wagering that I’ve been working on for the better part of a year, and another article will be evaluating the performances of the Chasers on ITV’s The Chase. However, current events have prompted me to write a Lightning Round article about this man, who has polarized fans of Jeopardy over the past two weeks:

The owner of this smile is Matt Jackson, a paralegal from DC who yesterday became the 5^th person ever to reach 10 wins, putting him 5^th on the all-time win list behind Arthur Chu (11), David Madden (19), Julia Collins (20), and, of course, Ken Jennings (74). Given Jackson’s performances so far, how many wins is he likely to finish his run with? Could we be looking at a new record holder?

I’ve taken a look at this sort of thing before, back in June of 2014 after Julia Collins had finished her 20 game run. I’m going to use the same methodology here: look at Jackson’s game situations heading into Final Jeopardy, and determine how often Jackson should be expected to win if he continues in that fashion.

In Jackson’s 10 games so far, he has achieved 8 lock games and 2 crush games heading into Final Jeopardy. The lock games are easy to deal with – Jackson wins those 100% of the time. That leaves the 20% of the time when Jackson is leading by more than 2/3s of his nearest opponent’s score. In order to lose a game that you are crushing heading into Final Jeopardy, two things need to happen: you need to respond incorrectly to Final, while your nearest opponent needs to respond correctly. So far, Jackson has a 60% correct response rate in Final Jeopardy. I’ll use the historical correct answer percentage for an average contestant in Final Jeopardy to determine the chance that his trailing opponent answers correctly, which is 48.8%. Since both events have to happen in order for Jackson to lose, we multiply the chances that Jackson misses (40%) by the chances that his opponent answers correctly (48.8%). This means that the chance that Jackson loses in a crush situation is 19.6%. Or, in other words, Jackson wins a crush 80.4% of the time.

So, 80% of the time, he locks up the game before Final and wins. 20% of the time, he has a crush heading into Final and wins 80.4% of the time. Combine those two probabilities, and you come up with an impressive 96.1% win rate. That is very impressive, close to Ken Jennings’ 97.0% win rate and well ahead of the third place win rate, David Madden’s 85.6%.

Does that mean he’s a threat to Jennings’ record? It’s not very likely. Jennings was very good but also very lucky, and outperformed his expectation (a mere 31 wins) by a large margin. A person with a 96.1% chance of winning would be expected to “only” win 24.56 games before losing. In Jackson’s case, we can add his 10 wins to that total to get our current estimate: an astounding but far from record-setting 34 games won. I predict his current chances of the setting the record at 7.2%: possible but unlikely.

Of course, this analysis is predicated on him keeping up his pace of dominating the first two rounds before heading into Final Jeopardy. Should he start to leave more openings for his opponents to catch him in Final, or (gasp) actually come into Final behind at some point, his expected win total would plummet. Still, as long as he keeps up this level of performance, I’d expect to see Matt Jackson on our screens for some time to come.

Lightning Round: 500 Questions

May 25, 2015 by Dave Leave a Comment

ABC’s latest Big Event Game Show Thing, 500 Questions, is currently in the middle of its nine night run. And while pundits are keeping tabs on whether or not the show will actually manage to ask 500 questions during its entire run (spoiler alert: no), a question asked on the LearnedLeague forums got my attention. A user asked what the chances were of a contestant actually completing the titular 500 questions. That sounds like something we can look into. So, we’re starting a new series here at Game Show Theory, The Lightning Round, devoted to questions about game shows that are interesting, but don’t really qualify for a full strategic breakdown.

Let’s have a quick refresher of 500 Questions’ rules. A contestant is asked trivia questions one at a time, up to a theoretical total value of 500 questions. Answering them correctly can earn money, which they secure after every 50 questions. However, if they ever miss three questions in a row, they’re off the show. There are some different types of question, and the presence of another player who may occasionally make life difficult for the contestant, but for our purposes we are going to ignore their effect on the game.

Question 5: How many fingers am I holding up?

So, how likely is it that a contestant sees all of their 500 questions? I know of no simple probability distribution to address this question, so we’re going to take a slightly more manual and iterative approach to the problem. We’re going to break the problem down by calculating the chance of a contestant surviving 1 question, 2 questions, 3 questions, and so on, up to the goal of 500 questions.

Let’s work through an example. Let’s assume a prospective contestant will give a correct answer to a question a respectable 60% of the time. Figuring out the chances of surviving the first two questions is trivial – it’s 100%, since there is no way to get three wrong answers in a row yet. The first chance of losing comes at 3 questions. The player would have to get the first three questions wrong in a row, which translates to 3 straight 40% shots:

The chances that the player would go three-and-out is 6.4%, meaning that 93.6% of the time they’re still in the game after three questions.

With that done, let’s work out the chances that the player bombs out after 4 questions. You might initially think at first that it’s the same as above, 6.4%, but actually there’s a couple of wrinkles we have to consider. First of all, we need to factor in the chances that they’ve already been defeated, since you can’t lose after 4 questions if you’ve already lost after 3 questions. Secondly, losing at 4 questions not only requires the contestant to have gotten questions 2, 3, and 4 incorrect, but also must have gotten question 1 correct. If Question 1 was answered incorrectly, there is no way the player can get three in a row wrong on question 4. Either they answer questions 2 and 3 wrong, in which case they’ve already been eliminated, or they answer one of those questions correctly, in which case Question 4 can’t be the third wrong answer in a row.

This gives us the following formula:

Factoring all that in, we now have a 3.6% chance of losing after question 4. Combined with the chances of losing after question 3, the total chances of survival are now a hair above 90%. If 10% of the time, the player will be out after only 4 questions, their chances of surviving 500 questions is not looking too strong.

Calculating the odds of losing on questions 5 and beyond can be calculated in the same way as question 4. We multiply the chance that we are still in the game at that point by the chance of answering one question correct and three questions wrong.

Question 500: Mark Burnett’s Beard. Seriously, WTF?

As you might imagine given the results so far, the results do not make pleasant reading for our hypothetical player. They only have a 50% of getting to question 19, well before they have the chance to make any money. They’re only going to be able to bank the money earned in their first 50 questions 14.8% of the time. And the chances of getting through all 500 questions? 0.0000003%. That’s about a 1 in 300 million chance, meaning they have as much chance of surviving 500 questions as they have of dying as a result of a shark attack. Put another way, our 60% contestant should stick to playing Powerball – they’ll have about twice the chance of winning the jackpot there.

What if we increase the contestant’s average question get rate? Here’s a chart that breaks down the chances of players of different strengths hitting the 25, 50, 100, 250, and 500 question milestones:

If a player wanted to have a 50/50 shot of getting through the 500 questions, they need to be very, very good. A player would have to get 88.37% of their questions right to stand a break-even chance of finishing the game, a number I would expect only trivia elite could get close to achieving.

One of the decisions that the producers of 500 Questions have made is to be outspoken in calling their contestants geniuses. They better be – only geniuses stand a chance of performing well.