
People who have made nearly $17.3 million from Jeopardy in the past 18 months, not including Colonial Penn Life kickbacks.
This Monday kicks off the 24th Jeopardy! Tournament of Champions, a two week sesquiennial bacchanalia of trivia where one lucky person gets to inscribe their name on the annals of Jeopardy! history. It’s the closest thing to an end-of-season playoff that we have in the American game shows, and in the spirit of March Madness I thought I’d put on my Nate Silver hat and take a shot at predicting who the winners would be. Let’s just ignore that in this case I’d be “predicting” the results of an event that was actually filmed a couple of months ago.
The Rules

There is no truth to the rumor that the first Tournament of Champions was held inside a seaside photo booth.
The tournament format, which was supposedly created by Alex Trebek himself, sees fifteen previous champions come back to play over two weeks. The fifteen participants are the winners of qualifying tournaments (currently the College Championship and the Teachers Tournament, previously winners of the Teen Tournament and the Seniors Tournament also got invites), and then enough champions who played since the last Tournament to fill in the remaining slots, ordered by number of games won, then amount of money won. The cut-off this year was Mark Japinga, who won 4 games and $112,600. (One 6-game champion was not invited back due to legal issues.) The first week sees the fifteen contestants placed semi-randomly (I’m pretty sure the contestants are seeded so that each game has one of the top five players, one of the middle five players, and one of the bottom five players) into five quarterfinal games. The five winners of these games are guaranteed passage to the next round, along with the four highest-scoring non-winners as wild cards. These nine players are again randomly drawn into three semifinal games, with the stipulation that you cannot play against someone you already played against in the first round. The three semifinal winners then face off in a two-day final, where the cumulative amount won on both days is used to determine the tournament winner.
It’s an interesting format because proper play requires a shift in strategy. Only the semifinal game is a traditional winner-take-all game of Jeopardy. In the quarterfinal, you don’t necessarily need to win the game, just have enough money at the end of the game to be one of the top four non-winners. This leads to some conservative wagering on Daily Doubles and in Final Jeopardy. The catch is that you are sequestered before you play your quarterfinal, so you do not necessarily know how much money would qualify you for the semifinal. There have been years where a score of $20,000 would have sent you home, and one year where multiple people finished with $0 but still made the semifinals. (I’ve done some work with this subject, which I’ll save for a later post.) The two-day final should be treated like a marathon compared to the usual format’s sprint, and strategic wagering in the first game could leave you with a strong platform to win, or leave you so far behind that it’ll take a miracle in the second game to come back.
Watson’s System
I was reading the Journal of Artificial Intelligence Research one night (as you do), and came upon a very interesting article written by part of the team that created Watson for IBM. In it, they discussed some of the various challenges they faced in building an AI capable of the strategy of playing Jeopardy!. To test out strategies, they built a game simulator where Watson would take on two “average” Jeopardy! contestants. They measured a contestant’s ability using two numbers, the percentage of clues that they attempt to buzz in on (called buzzing percentage), and the percentage of clues that they respond correctly to having buzzed in (called precision). Using data obtained from the Jeopardy! Archive, they determined that the average contestant attempts to ring in on 61% of clues, and answers 87% correctly. I wondered if I could use this same methodology to evaluate individual contestants’ skill as well.
Precision was easy enough to determine, just by observation. Buzzing percentage, however, is only an estimation. We have no way of knowing for sure how many clues a contestant buzzes in on. Using the Watson team’s methodology, we can make an estimate based upon how many clues a contestant successfully buzzes in on compared to their opponents and the number of “triple stumpers”, clues that nobody attempts.
Now, I had an issue with their buzzing model, and it might be one that you’ve noticed as well. Anybody who’s been on Jeopardy! or played a similar game knows that knowing the correct response is only half the battle. There’s also the dreaded lockout system that contestants have to conquer. Ever since the second season of the revived series in 1985, contestants have been forced to wait until the clue is read in its entirety by Alex before buzzing in. If they buzz in before the buzzer is active (represented by a set of lights around the playing board, not shown to the viewers), they are locked-out of buzzing for two tenths of a second. If they try to buzz in again during those two-tenths of a second, the lock-out resets. If you have ever seen a contestant frantically trying to ring in but nothing is happening, even if nobody else has rung in, it’s because they’ve fallen prey to the lock-out.
People have spoken of buzzer skill as a major part of a Jeopardy player’s ability. Some players manage to get in a rhythm with Alex’s cadence and seem to control the buzzer better than their opponents. The Watson team chooses to ignores that ability. It instead argues that a person who successfully buzzes in more just attempts to buzz in on more clues. It assumes that everybody has the same amount of “buzzer skill”; if more than one person attempts to buzz in, the successful contestant is simply a matter of chance.
To test this out, I built a program that took these two contestant metrics and simulated a game, using Eric Feder’s work on Jeopardy Win Expectancy as a starting point. When I ran simulations against the results of the last couple of tournaments, I was pleasantly surprised to see the simulation reasonably matching the results. Despite my misgivings, I feel comfortable moving forward with predictions on this year’s tournament.
Quarterfinal Matchups
Let’s take a look at the first five games. (Thanks to The Final Wager for revealing the matchups early, and thanks to Buzzerblog for the use of the contestant images.)
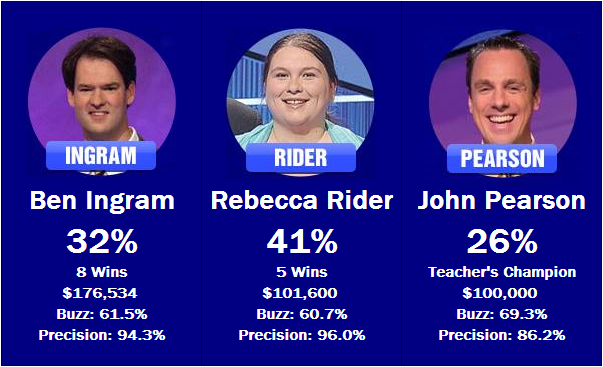
The first match will be a contrast in styles. Ben Ingram and Rebecca Rider both made their bones by being selective about their clue selection – they sport the two highest precision scores of the fifteen participants. John Pearson, on the other hand, buzzed in nearly 10% more often than either of his opponents, but wound up giving the wrong answer almost 10% more often as well. The system give a slight edge to Rider in this matchup, but Pearson should be selecting clues more often, giving him a higher chance of finding a well-timed Daily Double.
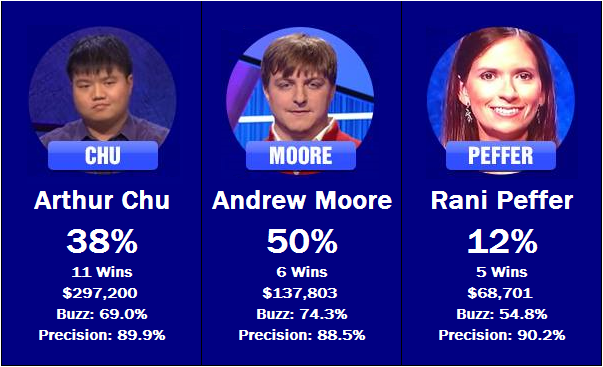
When I first calculated these statistics, I had to double-check Andrew Moore’s scores by hand to ensure their accuracy. I couldn’t believe that a fairly anonymous 6-time champ in a season full of memorable winners could have a buzzing percentage almost 5% higher than any of the other competitors, but the numbers checked out. While his precision is below average among tournament participants, it’s still good enough to give him the edge in this matchup, as well as in the overall tournament. However, he could find trouble playing against Arthur Chu, who the system is also keen on. Unfortunately, the tough matchup combined with her weak buzzing percentage does not bode well for Rani Peffer’s tournament chances.
20-game winner Julia Collins is given a slight edge against Joshua Brakhage and Jim Coury, although that’s more down to the quality of the competition than her own skill. Despite coming into the tournament as the favorite or co-favorite with Arthur Chu, the system sees Collins as merely an average ToC-quality player. If she were to play in either Tuesday’s or Friday’s game, she might have had a rough time making it to the second week. Incidentally, all three players are fairly conservative on the buzzer – expect a good number of Triple Stumpers.
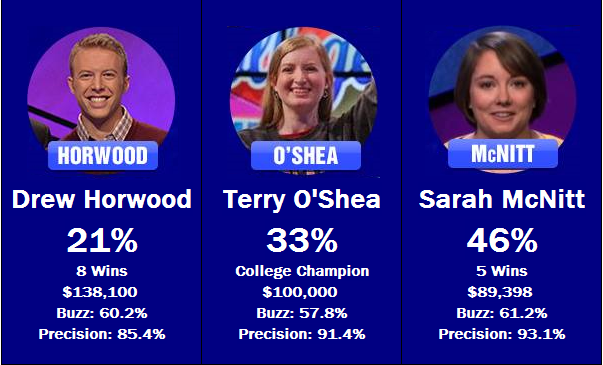
This matchup threatens to play out much like Wednesday’s, with three conservative buzzers, none of which have shown extremely strong game play, pitted against each other. Expect another game where a number of clues pass by unanswered. Sarah McNitt has the edge over Drew Horwood and Terry O’Shea in both buzzing and precision, and as such is given the favorite tag.
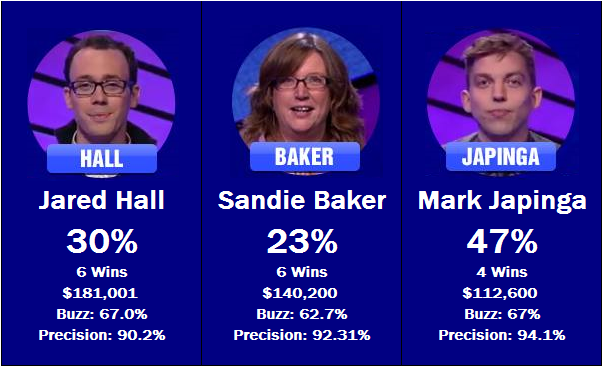
The week looks to end on a bang, with two strong competitors battling it out. Mark Japinga may have gotten a bit lucky to even be invited back to take part in the tournament, but now that he’s here he’s a serious threat to win the whole thing. Jared Hall is another strong player looking to go far. Sandie Baker is probably drew the worst game to play out of all the contestants – if she were playing on Wednesday or Thursday she might have been a favorite to win. Instead, she could get squeezed out early.
The Odds
Overall, I see this as a fairly wide open field. Thirteen people have a better than even money chance of making it to the semifinals, and the favorite’s chances of winning is only about 1 in 5. This could very well be the most exciting, unpredictable tournament in recent history.
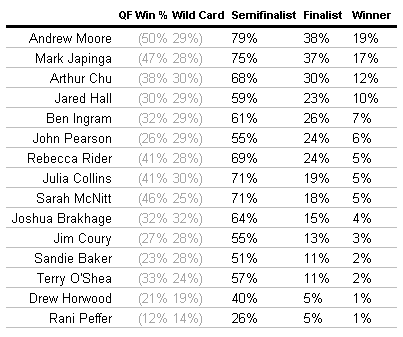
Note: There are two ways of making the semifinals, by winning your quarterfinal or qualifying as a wild card. We model the chances of each event happening (the percentages in gray), and sum the two together to determine the total chance that a contestant makes the semifinals.
Check back with us after every game next week for analysis and updates.



If you have video available, watch closely and most of the contestants will make it fairly obvious whether or not they are buzzing in.
You’re correct for the most part. Problem is that it still wouldn’t be accurate since some players are not very expressive when buzzing in. Plus, it would have required me to watch over 110 games while taking copious notes to prepare for this article. Ain’t nobody got time for that!
I find your analysis fascinating (and flattering!).
I am, however, mostly commenting to thank you for using the picture from my regular-season run, not the ToC photo. It’s a much better shot. (If I’m going to be on the Internet, I want to look pretty on the Internet, darn it!)